すみません、の剪断を表す行列がどうして[1 1 0 1]になるのかが分からなくて教えてほしいです...

Chapter 4 行列の積と変換の合成 | 線形代数のエッセンス

2023年02月22日　 @settent8938 様　

00:03:04 - 00:09:45

にあるように行列の積は右から左に読むので(AB)Cは「CしてABする」つまり「CしてBしてAする」を表していると思います。

Chapter 4 行列の積と変換の合成 | 線形代数のエッセンス

2023年02月22日　 @cmt-rt5ob 様　

00:04:06 - 00:09:45

πの色が変わったように感じてるの僕だけ？

Chapter 4 行列の積と変換の合成 | 線形代数のエッセンス

2023年02月22日　 @nona9Q_MC_𰻞𪚥 様　

00:09:17 - 00:09:45

～を見た方が分かりやすいです。

Chapter 3 行列と一次変換 | 線形代数のエッセンス

2023年02月18日　 @ave5163 様　

00:03:47 - 00:10:21

それ以外は全部そこから導けるんでね←主人公にちょっとした秘密を教える行商人のおっちゃん

Chapter 3 行列と一次変換 | 線形代数のエッセンス

2023年02月18日　 @名字名前-s8t 様　

00:03:48 - 00:10:21

の基底ベクトル)である必要はありません。~の話は、変換が1次変換でありさえすれば、変換を適用する前の座標系の基底ベクトルが、正規直交基底でなくても成り立ちます。

Chapter 3 行列と一次変換 | 線形代数のエッセンス

2023年02月18日　 @田中_田中 様　

00:04:03 - 00:10:21

での-1,2がここでのx,yにあたるものだと思います。

Chapter 3 行列と一次変換 | 線形代数のエッセンス

2023年02月18日　 @cmt-rt5ob 様　

00:04:22 - 00:10:21

ここ大笑いした

Chapter 3 行列と一次変換 | 線形代数のエッセンス

2023年02月18日　 @名字名前-s8t 様　

00:05:21 - 00:10:21

～を先に見てから、

Chapter 3 行列と一次変換 | 線形代数のエッセンス

2023年02月18日　 @ave5163 様　

00:05:23 - 00:03:47

の→のあとのx、yは前の［x、y］と無関係ですよね？

Chapter 3 行列と一次変換 | 線形代数のエッセンス

2023年02月18日　 @ckni-w4c 様　

00:05:38 - 00:10:21

すっごいどうでもいいですけど land なんですね

Chapter 3 行列と一次変換 | 線形代数のエッセンス

2023年02月18日　 @atridott 様　

00:06:05 - 00:10:21

「アグネス・L・ロジャース」とありますが正しくは「アグネス・K・ロジャース」です。訂正いたします。

Chapter 2 線形結合, Span, 基底ベクトル | 線形代数のエッセンス

2023年02月12日　

00:00:09 - 00:09:17

本筋と関係無いけどの人名を盛大に訳し間違えてるのめっちゃ気になる。

Chapter 2 線形結合, Span, 基底ベクトル | 線形代数のエッセンス

2023年02月12日　 @F-o 様　

00:00:09 - 00:09:17

の「 ([-0.8, 1.30]) != ([-3.1, -2.9])」 は、「基底ベクトルが異なる場合、ある座標を表すスカラ値のペアが異なることになる」っていう説明？「3マイルは4.8kmと表現できます」みたいな

Chapter 2 線形結合, Span, 基底ベクトル | 線形代数のエッセンス

2023年02月12日　 @mtaka84219 様　

00:02:40 - 00:09:17

線形だけに、筋が通っている

Chapter 2 線形結合, Span, 基底ベクトル | 線形代数のエッセンス

2023年02月12日　 @p0kMNyziCA-o5r 様　

00:08:50 - 00:09:17

ベクトルには和とスカラー倍による数学的構造が入っています。(あたりで述べられているように適切な和とスカラー倍が定義された集合の要素がベクトルです。)一方で配列は単なる数の組にすぎません。その数学的構造からベクトルは配列にはない様々な性質を持ちます(基底の存在など)。高校までの数学や物理ではこの辺りのことはそんなに見えてこないので同じことをしているように見えると思いますが。

Chapter 1 ベクトル | 線形代数のエッセンス

2023年01月27日　 @dhvhif1305 様　

00:01:25 - 00:09:10

ほとんど の解説と同じなんだけど、双六の「3マス進む」が「x方向に3、y方向に2進む」になったと考えて、「原点をふり出しにして全部の効果(ベクトル)を適用(加法や整数倍)させたら、最後にコマはどこにある？」ってイメージこの感覚を進めていくと、入試問題でよく見る平面ベクトルと図形の問題も「OAベクトルとOBベクトルという2つのサイコロをどう使えば目的地(求めたいベクトルの終点)に行ける？」みたいに読めて、割とすんなり解けた(あくまで、数学が好きな文系学生だった人間の感想です)

Chapter 1 ベクトル | 線形代数のエッセンス

2023年01月27日　 @n.liquet982 様　

00:04:58 - 00:09:10

感動して泣いちゃった

Chapter 1 ベクトル | 線形代数のエッセンス

2023年01月27日　 @ninjin_maaaru 様　

00:05:12 - 00:09:10

このアニメーションってPythonで出力してたのか……

Chapter 1 ベクトル | 線形代数のエッセンス

2023年01月27日　 @おののコマネチ 様　

00:08:36 - 00:09:10

から

【視覚的に理解する】フーリエ変換

2023年01月16日　 @kt-en6rp 様　

00:00:01 - 00:17:27

信号の周波数＝巻き付けの周波数これめっちゃナイキスト線図

【視覚的に理解する】フーリエ変換

2023年01月16日　 @すらまる-r4n 様　

00:04:24 - 00:17:28

媒介変数のやつだ

【視覚的に理解する】フーリエ変換

2023年01月16日　 @TT-lq4do 様　

00:04:24 - 00:17:28

ここがよくわからない。図を質量のあるワイヤーみたいなものと捉えて、ワイヤーの巻きつけ度合いによって重心が動くって説明は理解できるけど、だとしたらなんでここで重心がワイヤーを離れるの？直感的には重心は第四象限の黄色線のどこかにあると思ってしまうんだけど。

【視覚的に理解する】フーリエ変換

2023年01月16日　 @satounasi0097 様　

00:05:20 - 00:17:28

万華鏡写輪眼すぎる

【視覚的に理解する】フーリエ変換

2023年01月16日　 @トガっ 様　

00:06:18 - 00:17:28

耳塞いでるのカワイイ

【視覚的に理解する】フーリエ変換

2023年01月16日　 @labsakura4104 様　

00:10:10 - 00:17:28

ローパスフィルターですね！！すごい！！

【視覚的に理解する】フーリエ変換

2023年01月16日　 @matsu_photo 様　

00:10:30 - 00:17:28

真実の方向を向いている嘘ですっていう言葉すごくいい表現

【視覚的に理解する】フーリエ変換

2023年01月16日　 @NaN-us1cp 様　

00:10:48 - 00:17:28

うーん、いやこれはちょっと嘘なんですけど

【視覚的に理解する】フーリエ変換

2023年01月16日　 @名字名前-s8t 様　

00:10:58 - 00:17:28

基礎知識が足りなくてここから何言ってるのかわからん状態だった

【視覚的に理解する】フーリエ変換

2023年01月16日　 @藁山花太-j5s 様　

00:11:24 - 00:17:28

ここまでは理解できた()

【視覚的に理解する】フーリエ変換

2023年01月16日　 @コウ-o6n 様　

00:11:26 - 00:17:28

「微積分でよろめく人は恐怖を感じるかもしれません」まさに恐怖を覚えている最中だったので心を読まれたようで笑ってしまった

【視覚的に理解する】フーリエ変換

2023年01月16日　 @田中太郎-z4f1p 様　

00:14:19 - 00:17:28

まで全く分からないことだらけだったのになぜか最後まで見てしまう、見れてしまうすごい動画

【視覚的に理解する】フーリエ変換

2023年01月16日　 @kt-en6rp 様　

00:17:27 - 00:17:28

こんな発想何食って生きてたら思いつくんだよ　霞か？

なぜ円錐の断面は楕円になるのか

2022年11月15日　 @yabe_chikoku 様　

00:03:51 - 00:10:36

動画を見ながら思わず、あっ、と声が出てしまいました。

なぜ円錐の断面は楕円になるのか

2022年11月15日　 @kingofm2010 様　

00:05:40 - 00:10:36

とかの細かい所も証明するのが本当に丁寧。直感的にピンと来るし、飛ばしてもおかしくなさそうなのに

なぜ円錐の断面は楕円になるのか

2022年11月15日　 @Minty_HAL 様　

00:06:16 - 00:10:36

美しスギィ！

なぜ円錐の断面は楕円になるのか

2022年11月15日　 @kkofu 様　

00:07:26 - 00:10:36

ここ史上最高に気持ちいい笑直線だと？！！！

なぜ円錐の断面は楕円になるのか

2022年11月15日　 @ケムケムたちんば犬 様　

00:07:35 - 00:10:36

の左の数式が気になります。

なぜ円錐の断面は楕円になるのか

2022年11月15日　 @あお-q9y5n 様　

00:10:00 - 00:10:36

① 衝突という力学的な問題を幾何学的な問題として解釈するための数学的なアプローチ。発想しろと言われれば難しいけどそういうものと提示されたら理解するのはできるはず。

【円周率と衝突するブロック２】 光との関連性

2022年10月08日　 @qt702 様　

00:01:15 - 00:03:30

② 衝突を表すy=xの直線を入射角と反射角が等しくなるようにうまく調整しているわけだけど、これも発想するのは難しくとも理解するのはそれほど難しくないはず。

【円周率と衝突するブロック２】 光との関連性

2022年10月08日　 @qt702 様　

00:03:30 - 00:10:45

からのご褒美タイム、気持ち良すぎるだろ…！

【円周率と衝突するブロック２】 光との関連性

2022年10月08日　 @creations1259 様　

00:10:38 - 00:13:30

③ この動画の最も美しい部分。入射角と反射角が等しいことから「反射しているのではなく反転世界で直進している」として②で調整した直線とx軸とのなす角Θとその半円の関係性が見える。

【円周率と衝突するブロック２】 光との関連性

2022年10月08日　 @qt702 様　

00:10:45 - 00:13:30

及び概要欄です。

【円周率と衝突するブロック２】 光との関連性

2022年10月08日　 @k.n.6206 様　

00:11:57 - 00:13:30

「最も偉大な鼻の低い数学者」なんのことかわからなかったから調べたけど、第一次世界大戦の傷痍軍人なんだね…当然だけど、この時代、数学者も戦争に駆り出されてて壮絶だなと思う。

マンデルブロ集合を越えて

2022年09月11日　 @やこす-t4x 様　

00:03:44 - 00:27:15

動画見返しててなんでマンデルブロ集合がカージオイドなのかようやく理解した、円の先にもう一つ円を用意して連動させながら回転させるってまさにカージオイドの書き方なんだ

マンデルブロ集合を越えて

2022年09月11日　 @r-00x28 様　

00:04:37 - 00:27:15

銀河の形に似てるな

マンデルブロ集合を越えて

2022年09月11日　 @toknsittoknsit3527 様　

00:07:02 - 00:27:15

どうやら、ｩｱ全然自明ではないのですが、

マンデルブロ集合を越えて

2022年09月11日　 @名字名前-s8t 様　

00:17:31 - 00:27:15

すごい。…のだろうけど、理解が追いつかず1回見ただけでは感動できなかった

マンデルブロ集合を越えて

2022年09月11日　 @mmiyake8272 様　

00:20:45 - 00:27:15

どれだけ拡大しても、「全ての色が見える」か、「一色」になる。フラクタル図形のもつ、自己拡大性という視覚での感覚と、数式での記述が一致した。うろこが落ちた。

マンデルブロ集合を越えて

2022年09月11日　 @merdekaataumati1949 様　

00:22:06 - 00:27:15

\ﾄﾞｯ/

ニュートン法と美しきフラクタルの世界

2022年08月10日　 @reenn6766 様　

00:01:16 - 00:24:18

コメントでのAbel-Ruffiniの定理の話をしているところで、画面上ではsinやexpなどの超越関数を含めているので「超越的」というのが正しいのではないかという良い指摘がありました。Abel-Ruffiniの定理は代数的公式についての定理で、ここではそれに加えてsinやexpなどの関数によっても公式が得られないということを画面上のテキストで説明しています。この箇所については元の英語版の動画にほぼ忠実に翻訳されており、ナレーションでは直前に「代数的な解の〜」と言っていますがそれに続く「そこそこ広範囲の〜」という部分がこのコメントに関係のある箇所でこれらの超越関数を含めた表現になっています。元の動画も翻訳版もなるべく伝わりやすい表現をするために、詳しい方にとっては厳密でなかったり物足りなかったりする場合があります。

ニュートン法と美しきフラクタルの世界

2022年08月10日　

00:05:11 - 00:24:18

のアーベルールフィ二の定理のところで、五次方程式が代数的に解けないということについて、英語で「＋、ー、×、÷、累乗根では解けない」としているのは正しいと思いますが、そのあとの「exp,log,sin,cos」の箇所は「代数的操作」ではない「超越的操作」なので、正しくないのでは？と思いました。

ニュートン法と美しきフラクタルの世界

2022年08月10日　 @blackbox4283 様　

00:05:11 - 00:24:18

「そのうち開けたいパンドラの箱」すこ

ニュートン法と美しきフラクタルの世界

2022年08月10日　 @kokikawaguchiMusic 様　

00:05:20 - 00:24:18

最初にニュートン法が紹介された時天才じゃんと思ったけど、でy方向にシフトしただけでうわっと叫んでしまった数学浅瀬チャプチャプマンには深すぎて溺れるがとても興味深い今回も難解なテーマをわかりやすく説明していただきありがとうございます

ニュートン法と美しきフラクタルの世界

2022年08月10日　 @swaht9142 様　

00:08:40 - 00:24:18

「呑気な島の実数の関数」とかいう地球史上この動画でしかお目にかかることがなかったであろう表現がずっと耳にこびりついてる

ニュートン法と美しきフラクタルの世界

2022年08月10日　 @仮名ろはん 様　

00:09:42 - 00:24:18

から分けわかめ

ニュートン法と美しきフラクタルの世界

2022年08月10日　 @ソファ-z9f 様　

00:10:00 - 00:24:18

なんかちょっとマンデルブロ集合っぽい形になってきてるな

ニュートン法と美しきフラクタルの世界

2022年08月10日　 @yuuki246 様　

00:11:09 - 00:24:18

ここ感動した

ニュートン法と美しきフラクタルの世界

2022年08月10日　 @mui_nyan 様　

00:12:10 - 00:24:18

ぶち上がりポイント

ニュートン法と美しきフラクタルの世界

2022年08月10日　 @einoue3576 様　

00:12:13 - 00:24:18

感動の瞬間

ニュートン法と美しきフラクタルの世界

2022年08月10日　 @azuma3520 様　

00:12:16 - 00:24:18

〜あああああああ！！！！！！頭がおかしくなる！頭がおかしくなる！なんで同じなの?！終わりがない！！怖い！！怖いよ！！助け

ニュートン法と美しきフラクタルの世界

2022年08月10日　 @佐藤紫央-d7j 様　

00:12:20 - 00:24:18

は？

ニュートン法と美しきフラクタルの世界

2022年08月10日　 @lareseng 様　

00:15:03 - 00:24:18

から　「ある回数で止めて→無限のディテイル」は違う気がする

ニュートン法と美しきフラクタルの世界

2022年08月10日　 @ああ-i8c2d 様　

00:16:05 - 00:24:18

これがどれほど驚くべきことか見進めて行くとじわじわ実感できてくるのがいいですね…何だか背筋がゾワっときてしまう…

ニュートン法と美しきフラクタルの世界

2022年08月10日　 @ittitis6084 様　

00:17:38 - 00:24:18

賽の河原

ニュートン法と美しきフラクタルの世界

2022年08月10日　 @名字名前-s8t 様　

00:19:04 - 00:24:18

なんで雫型‪💧‬なんだ？

ニュートン法と美しきフラクタルの世界

2022年08月10日　 @転ばし屋-v5x 様　

00:19:30 - 00:24:18

から視覚的には爆発に見えるかもだけど、常に一定の割合で広がってそう

ニュートン法と美しきフラクタルの世界

2022年08月10日　 @ああ-i8c2d 様　

00:21:30 - 00:24:18

この疑問が一番気になるところだけど、次回までのお楽しみか〜

ニュートン法と美しきフラクタルの世界

2022年08月10日　 @BombMillton 様　

00:22:21 - 00:24:18

素敵ですね

ニュートン法と美しきフラクタルの世界

2022年08月10日　 @tta6119 様　

00:23:00 - 00:24:18

ただ、 からで泣ける様になって来た。

ニュートン法と美しきフラクタルの世界

2022年08月10日　 @chainsaw3014 様　

00:23:19 - 00:24:18

h😂

なんで球の表面積って円の面積の4倍なの？

2022年07月17日　 @比嘉景敏 様　

00:00:29 - 00:13:48

〜もうすでにわからん球が長方形になるんや

なんで球の表面積って円の面積の4倍なの？

2022年07月17日　 @イケメンハンサム-k9p 様　

00:01:20 - 00:13:48

(1)

なんで球の表面積って円の面積の4倍なの？

2022年07月17日　 @moooooo7617 様　

00:02:04 - 00:10:40

ものすごく共感します。この快感って、算数、数学を学んだものしか味わえないんでしょうね。しかも、今はこのようなイメージ動画でかっちりと感覚を直感的につかむことができる。良い時代になったものです。私のような、思いっきし文系の人間にも数学の素晴らしさが味わえますから。小中学生では、まででも、十分に楽しめると思います。

なんで球の表面積って円の面積の4倍なの？

2022年07月17日　 @johan_reebelt 様　

00:02:05 - 00:13:48

あたりの表面積が等しい話なんですが、世界地図でよく言われる「極付近は引き伸ばされて大きく見える」と言う話が、実は面積自体は実際のものと変わらないんですかね

なんで球の表面積って円の面積の4倍なの？

2022年07月17日　 @こんでいめんと 様　

00:02:10 - 00:13:48

ごめんなさい。辺りでついていけなくなりました。。

なんで球の表面積って円の面積の4倍なの？

2022年07月17日　 @km-sf1hz 様　

00:02:45 - 00:13:48

この詳細の味付けが全体の議論の遠巻きの構造と同じくらい面白い

なんで球の表面積って円の面積の4倍なの？

2022年07月17日　 @beanmeet 様　

00:03:51 - 00:04:01

数学の問題を解く時は名前を付ける所から始めるのに損は無いです

なんで球の表面積って円の面積の4倍なの？

2022年07月17日　 @beanmeet 様　

00:04:01 - 00:13:48

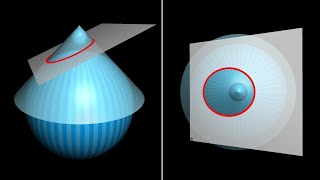
［外側の円の半径はRsin(θ+dθ)になるけど、dθはとてもとても小さいから、あまり気にしなくてよい。 ］

なんで球の表面積って円の面積の4倍なの？

2022年07月17日　 @さしす-q2y 様　

00:04:13 - 00:12:08

もう無理

なんで球の表面積って円の面積の4倍なの？

2022年07月17日　 @ssinn0801 様　

00:04:38 - 00:13:48

「これは本質情報ですが」でニヤッとしてしまった

なんで球の表面積って円の面積の4倍なの？

2022年07月17日　 @しの-y8r 様　

00:05:33 - 00:13:48

の小さな三角形がゼロでない面積を持つならばその頂点の接線と三角形の斜辺とは一致しませんが、この議論では小さな三角形の斜辺を縮める極限をとる前提があるので、図の半径の極限は”接線を通る半径”に一致します。このとき、後の議論で”直角”としてとる角度も極限で直角に一致するので、この議論においては先に小さな三角形の頂点を通る半径を接線を通る半径扱いできるというわけです。

なんで球の表面積って円の面積の4倍なの？

2022年07月17日　 @absant2913 様　

00:05:39 - 00:13:48

ここで使われている映像表現のような、変数の変化による視覚的な変化を自身の頭の中でイメージする能力、つまり何かが変化した時、伴って変化する全てを含めた全体像を連続ししたビジュアルとして捉える能力は、学習の早い段階で獲得しておくことで非常に役に立つと思います。実際、中学受験をするような小学生の一部は、すでにこうした能力を身につけ始めていて、あらゆる問題を解決する際に、問題の裏に隠された「こうなったらこうなる」を見つけだすのが非常にうまいのです。

なんで球の表面積って円の面積の4倍なの？

2022年07月17日　 @ryojitakei71 様　

00:05:54 - 00:13:48

意外とこの一言が大事だったりも…

なんで球の表面積って円の面積の4倍なの？

2022年07月17日　 @さかもとさん-h7h 様　

00:06:56 - 00:13:48

d/Rじゃない？

なんで球の表面積って円の面積の4倍なの？

2022年07月17日　 @pyonkichi56 様　

00:07:12 - 00:13:48

と同じように相似な△を考えると、小さい△は大きい△のdθ倍になっている。陰の部分の◎の幅、つまり小さい△の横幅は、大きい△の縦幅のdθ倍だから、Rcosθ×dθ=Rdθcosθ

なんで球の表面積って円の面積の4倍なの？

2022年07月17日　 @さしす-q2y 様　

00:07:12 - 00:12:22

R分のd ですよね？

なんで球の表面積って円の面積の4倍なの？

2022年07月17日　 @SATOKAGE 様　

00:07:13 - 00:13:48

のところ、分母と分子が逆じゃないでしょうか？

なんで球の表面積って円の面積の4倍なの？

2022年07月17日　 @jinhiroaki 様　

00:07:13 - 00:13:48

は R/d ではなく d/R ですかね。

なんで球の表面積って円の面積の4倍なの？

2022年07月17日　 @ごはんがすすむくん 様　

00:07:14 - 00:13:48

R/dじゃなくて、d/Rかな

なんで球の表面積って円の面積の4倍なの？

2022年07月17日　 @斎藤ナオト 様　

00:07:15 - 00:13:48

極端？に言えばこの世に「曲面」は存在せず、極々小さな平面の集まりである。ってこと？

なんで球の表面積って円の面積の4倍なの？

2022年07月17日　 @barusee_freedom 様　

00:08:45 - 00:13:48

ここまで見て、やっぱり微積の応用になるのねって思った。これ見て思い出したけど、陸上トラックのスタートラインの引き方(一万メートル走とかの)もそうなるのかなあ…。あれ?そうなると台形の面積の公式も微積の応用なの？寝られなくなったw。

なんで球の表面積って円の面積の4倍なの？

2022年07月17日　 @johan_reebelt 様　

00:08:52 - 00:13:48

これ台本なのか、言い間違えなのかが気になる

なんで球の表面積って円の面積の4倍なの？

2022年07月17日　 @figen498 様　

00:09:40 - 00:13:48

あと、の翻訳バージョン限定(?)のメタツッコミ面白くて好きです。

なんで球の表面積って円の面積の4倍なの？

2022年07月17日　 @yp_rioya 様　

00:10:16 - 00:13:48

11:28 (2)

なんで球の表面積って円の面積の4倍なの？

2022年07月17日　 @moooooo7617 様　

00:10:40 - 00:11:28

なんで球面にワッカがあるんだよ？

なんで球の表面積って円の面積の4倍なの？

2022年07月17日　 @八区好男 様　

00:10:40 - 00:13:48

53位

なんで球の表面積って円の面積の4倍なの？

2022年07月17日　 @兵衛しのん 様　

00:10:44 - 00:13:48

(3)

なんで球の表面積って円の面積の4倍なの？

2022年07月17日　 @moooooo7617 様　

00:11:28 - 00:13:48

Q1球面上の◎の面積を求めるためには、円の半径と、◎の幅がわかればよい。内側の円の半径は、球を真横(y軸方向)から見て、Rsinθだから、その円周は半径に2πをかけて、2πRsinθ

なんで球の表面積って円の面積の4倍なの？

2022年07月17日　 @さしす-q2y 様　

00:11:39 - 00:04:13

Q2陰の部分の◎は、内側の円の大きさは球面上の◎と同じだけど、内側の円と外側の円の間の距離が短い。

なんで球の表面積って円の面積の4倍なの？

2022年07月17日　 @さしす-q2y 様　

00:12:08 - 00:07:12

Q3陰の部分の◎の面積は、二倍角の公式を使って2πR²dθsinθcosθ=πR²dθsin2θとかける。これとQ1 で求めた球面上の◎の面積: 2πR²dθsinθ を見比べると、ちょうどθを2θに変えて2倍したものになっている。

なんで球の表面積って円の面積の4倍なの？

2022年07月17日　 @さしす-q2y 様　

00:12:22 - 00:12:44

Q4北極(x, y=0, z=R)から緯度dθの間隔で地球をスライスして、たくさんの◎にわける。そして、北極点に一番近い方から1番、2番、...と番号をつける。

なんで球の表面積って円の面積の4倍なの？

2022年07月17日　 @さしす-q2y 様　

00:12:44 - 00:12:59

Q5すると、北半球の全部の陰を覆う面積は、偶数番目だけの球面の◎の面積の合計の½ になる。つまり、円の面積の2倍は偶数番目だけの球面の◎の面積の合計と等しい。また、偶数番目だけの球面の◎の面積の合計と奇数番目だけのそれは等しい。

なんで球の表面積って円の面積の4倍なの？

2022年07月17日　 @さしす-q2y 様　

00:12:59 - 00:13:48