動画数:59件

ファッションモデルの機械学習モデルのような事を話す場合はGPTは混乱するのだろうかいやまあ人間も混乱する気はするが…

1980年代に大学生の僕はそのアプローチでのAIの勉強をしていました。LISPやPrologなどのプログラミング言語を駆使してモデルを構築しようと試みられた時代です。当時それらの言語に最適化した専用のコンピュータまで開発されましたが、結局実用的なAIはできなかった。その頃既にニューラルネットワークの基礎理論はありましたが主流ではありませんでした。昨今のAIの隆盛を見ると、新しい時代が来たことをしみじみと感じます。わかりやすい動画での解説ありがとうございます。

ヒトラーを足すとかいうパワーワードで笑ってしまった

「ドイツ-日本」という地域の差に「スシ」を加えると、「ソーセージ」が得られる。面白い!わかりやすい!ベクトルで考えると似た要素同士が近い距離に集まって、要素と要素の関係性が「特徴」として類似のベクトルを作り出す、なるほどー。

内積を二つのベクトルがどれくらい揃っているかを表す尺度とすると、内積はベクトルの大きさにも依存するのでのような比較には向かないかと思うのですが、実際には正規化など行われているのでしょうか?数学には自信がなく、誤っていたらすみません。ベクトルの大きさが意味することがわかると理解できるかもしれませんし、次回も楽しみです!

Unembedding matrix(アンエンべディングマトリックス)を表現行列ってどこかで言ってたのを見たような聞いたような…。忘却の彼方。

ソフトマックス関数が量子力学の各エネルギー固有値に粒子が存在する確率を表す関数p_i=exp(-βE_i)/(Σexp(-βE_i) と完全に同じ形なのおもろい

メモ Temperature

個人的メモ: から連続関数

からの、「-1/2から1/2の間の一様分布を持っている確率変数」との和の分布を作る操作が、積分回路に電気信号を流す操作にとても似ていて面白かったです。どっちも積分なんだから当然だけど⋯。つまり複数の積分回路を直列に繋いで信号を流すと、繋いだ積分回路の数次第で、出力はベルカーブに近づいていくはず。入力がどんな波形だとしても。(理想的には)

なんで断面の面積をさらに√2で割るのか、最初疑問だったけど多分わかった

この式みて、大体わかった。指数関数の掛け算って、指数部分の足し算だよね

から本題❤
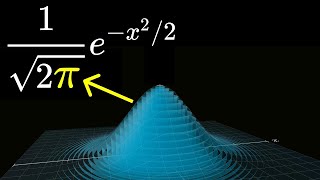
「『自然科学における数学の不合理な有効性』というフレーズを聞いたことがあるかもしれません」←聞いたことがなかった

カイトをフォローしてるから

(1)

(2)

元の数式はそこそこわかり、いくつく先も直感では正しいとわかっているのに、その間はどうやらトリックが必要だとわかると、自分で解決するのはほぼ無理で行き詰まる。そんなときは教授に直接聞くかクラスの一番賢い奴から手ほどきを受けるかする必要が有るのだが、動画で説明してくれて、それが良くわかるのに驚くよ。

高さがなぜ e^-(r^2) になるんですか??

この辺の話を代数的処理(積分における変数変換)も使って併せて示せば、係数2πが極座標系から自然と出てくるのが明瞭になるのではないかと思います。実用的な知識にもなるのではないかと思います。

-e^(-r^2)の導関数が2r・e^(−r^2)になる理由がわからない

分母は2πσ^2が正しいです

言葉で説明するとき、 xとyが独立 としか条件のことを言っていないけれど、そこから飛躍して関数を積の形に変数分離できると仮定しているここで他でもない積の形にxとyを変数分離できるとしているところが全てだと思う積の形という指定がなければ無数に関数が存在するだから、ガウス分布が導かれる理由を説明するにはなぜ積の形に変数分離されるのかを説明できなければいけない別にxとyが独立であるという条件が満たされれば良いのなら積でなくてもいいのでは?という意見に対して何か説明できてこそ、ガウス分布を理解していると言える

ここがどうしてf(x,y)=g(x)h(y)になるかがわからないです、、、別にg(x)+h(y)とかでもいいんじゃないんですか?教えて頭いい人!
動画始まって早くもめちゃくちゃ興味深いこと言ってて震えた

standard deviationのdではないでしょうか?

からの視覚化が分かりやすすぎるこの視覚化を作るために一体どれだけの時間とセンスが必要なのか…

ここ見たら分かりますけどその2はσの方から出て来たものですよ

ここ、考えてみれば殆ど1か6かのコイントスを行ってる感じだから5の間隔で確率分布が大きくなるのは当たり前なんだなあ 言うなればN=10じゃ解像度が足りてないとでもいうか

314159と271828と161803の意味は分かるけど466920の意味だけ分からない……

零一円周率自然対数の底第一ファイゲンバウム定数黄金比

PDF?!

「野生の確率密度関数」ってワード好き

野生の確率密度関数ww🤣

同じ無限でも可算と連続で話が変わるのが興味深いですね。hは有理数であると仮定した場合はどうなるのだろう……?

「有り得る結果はたくさんあるのだけれど、それら一つ一つの確率はゼロ」まさにずっと疑問に思っていたことに当てはまる表現に出会ってスッキリしました

/

〜 ドミノ・ピザ

「もしよかったらお好きなプログラミング言語で確かめて」普通にある前提で言うんじゃないよwMSX-BASIC。

「レンズの焦点をずらした時により近いようなぼかしの効果が得られます」焦点が合ってない時のボケ方は、中心に重み付けした状態に近いわけではありません。参照するグリッドが円形(レンズの絞りの形)で、重み付けが無く、そして範囲が広い場合に近いボケ方になります。玉ボケの写真を見ると、重み付けにより中心が濃いなんてこともなく、単純に濃淡の無い(重み付けの無い)円になっているのがわかると思います。焦点が合ってない時のようなぼかしをする時に、ガウスぼかしを使うのは間違い。

有名な「ガウスぼかし」って、そういうことだったのか!

日本語の高速フーリエ変換これが一番良いと思う。

実際に計算して係数c0,c1を導出するときに、この値が複素数になりそう。問題ないの?教えてえろい人
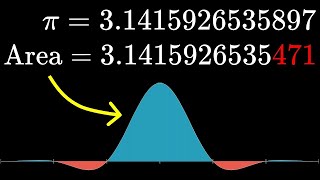
各色の部分の総面積って発散するんじゃなかったっけ・・・?

平均ってどう計算するんですか?

ここからの内容は

なるほど、ここで微分すふからシグモイド関数よりもReLU関数を使った方が計算が簡単になるのか それでReLUの方が上手くいく場合もあるってことね

これは、各層における重みを、そこで大きさが最大となる重みの値×何かしらの定数で規格化した値によって調整するということでしょうか?
