動画数：59件
実際に見たことのあるやり取り：「ベクトルって何？」『ベクトルは、ベクトルです』
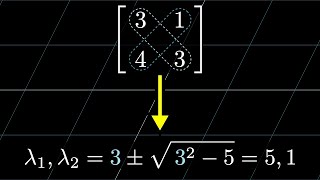
1)の性質はn次固有多項式のn-1次項の係数についての恒等式から求められます
(1)
(3)
4:46 (2)
途中で止めるのおもろい
ピ↓（ピッ↑）
の右下の文字、あまりにも一瞬でわかりづらいので、文字を書き起こしておきました。興味深いことに複素数平面でiの掛け算が90度の回転のように見えることはiが2次元の実ベクトルのこの変換の固有値であることと関係しています。この詳細はこの動画の範疇を超えていますが、複素数の固有値は変換におけるある種の回転に対応していると言えるでしょう。
ここ3人目だけまだ動画見てないの可愛い
からのアニメーションは、背景に元のグリッドを残した方が分かりやすいかと思います。というか、自分はここで一回躓きました。あくまでJenniferが表そうとしているベクトルを、「私たち」の座標系で見た時のベクトルが、行列の積の結果です。
gridの翻訳/言語の翻訳（）ベクトルの基底変換（動画前半）/線形変換の基底変換（動画後半）の違いをしっかり区別することがポイントだと思う
「こら！この出力は殆どのニューロンが0で！このニューロンだけ1になるようなアクティベーションになってないとダメで！」まではそこそこ怒ってるのに、「君の出した答えは全くのゴミです。」で急に冷静になって耐え切れなかった。
ひどい…
なぜコスト関数の入力が1万3千と説明されているのでしょうか？ニューラルネットワーク側の出力の数、つまり10という数がコスト関数側の入力数になるのではないですか？
〜
このラベル付けをシャッフルした話だけ意味わからん
最後の間違ったラベルを付けて学習させてもうまくいったってのは、つまりライオンの画像を見てフォークと分類できるようなモデルが作れたってこと？
メモ
難しくなってきた
誤って5億年ボタンを押してしまった際はこれで時間を潰そうと思いました
バイアスのベクトルの最後の添え字はnではなくkです
ここ b0...bn だとW*aの計算後に出る列と合わなくないですか?
えらく単純化したなぁ。これでいいのか。
【量子力学】〈行列力学と波動函数〉〈ライブラリの✨最適化✨『量子コンピューター重ね合わせ❗️💡の✨原理』〉『出汁醤油と出汁道楽✨』
)〈青チャート、数研出版〉にあります。
偶数の場合は ですでに説明されていますf(x) = Π[n=0..2000] (1+x^n) として(1/2) (f(1) - f(-1)) = 2¹⁹⁹⁹ です
, 行列の3行目は正しくは"v1 * w2 - w1 * v2"です。
〜について、そもそも3次元から1次元への変換が線形であることとは何なのでしょう。(以下、次元をDと略します)多分、このシリーズの内積で出てきた、「2D→1Dの変換について、2次元平面の直線上の等間隔な点が、変換後も等間隔になるなら線形」に似たものがあるんでしょうね。もし「ある3D→1Dの変換が、3次元空間内の直線上の点を等間隔なままになるように移す時、その変換は線形」なら、体積を考えることで線形であることが分かりますね。
の変換が線形であることの証明は本家のコメ欄で解説されてるからわからない人いたらみてみるといいかもしれない。
からの説明で「P,V,Wで作られる平行六面体の体積～」とありますけどなぜ[x,y,z]でなくPとしているのでしょうか？流れでは[x,y,z],V,Wで作られる平行六面体の体積を考えようとしていたと思いますしそもそももとの動画でもPとは言っていないですよね？